Lecture : Linear Discriminant Analysis

PCA vs LDA

Principal Components Analysis finds the direction of maximum variance for a dataset XX.
If each datapoint x∈Xx \in X falls into one of a distinct number of classes ci∈Cc_i \in C , PCA does not utilise this information to better separate the data.

LDA

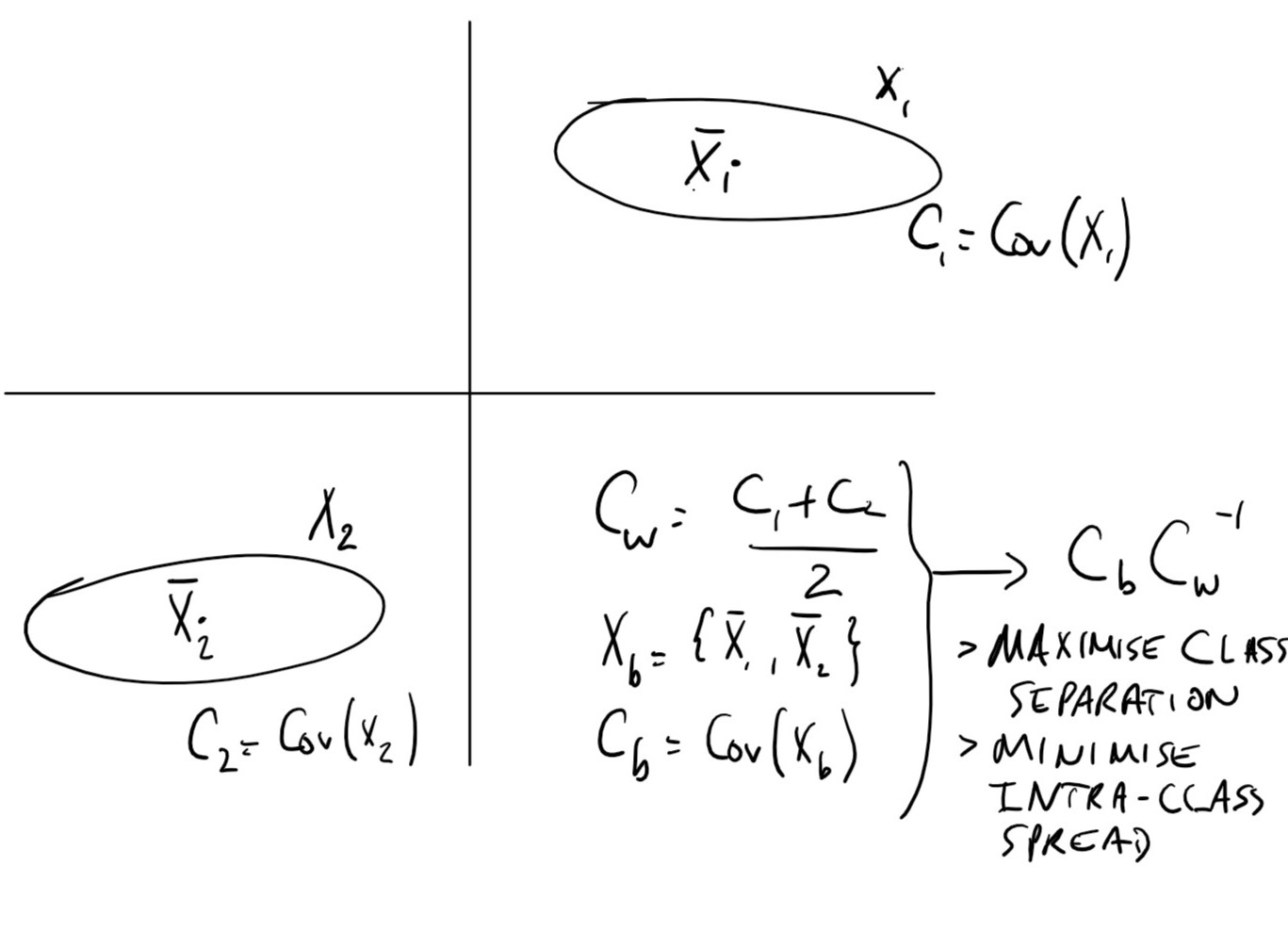
In this case where we have a dataset XX where each point belongs to one of KK classes, let XkX_k be the set of data points in XX that belong to the class ckc_k.

X=X1∪X2∪⋯∪XKX = X_1 \cup X_2 \cup \cdots \cup X_K

Let CKC_K be the covariance matrix of the dataset XKX_K, we define the average within-class covariance matrix CwC_w as:

Cw=C1+C2+…CKKC_w = \frac{C_1 + C_2 + \ldots C_K}{K}

Let XbX_b be the a KK row matrix where the kthk^{th} row is the average of the vectors in XkX_k. The between-class covariance matrix is the covariance matrix Cb=Cov(Xb)C_b = \text{Cov}(X_b)

In order to separate the classes we want to find a direction in the vector space that simultaneously:

  1. Maximises the between-class variance CbC_b
  2. Minimises the within-class variance CwC_w

The vector that satisfies these requirements is the eigenvector of CbCw−1C_bC_w^{-1} corresponding to the largest eigenvalue.

Diagrammatic Example

LDA vs PCA

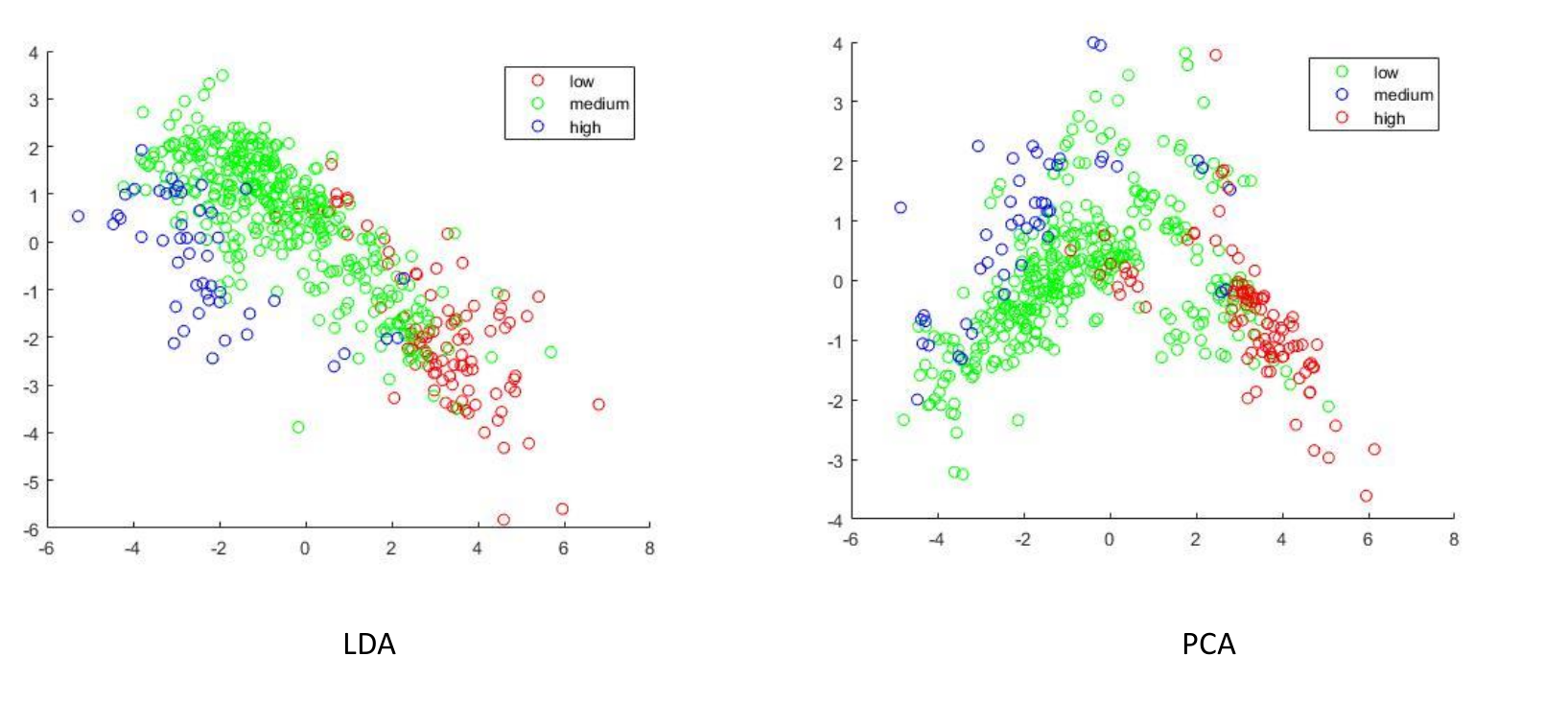
Here you can see that the split of the data is much more defined using LDA with entire sections being entirely populated by a single class.

≡