Lecture 2: Randomised Algorithms

Categories of Algorithms

• Divide and conquer
  • e.g. quicksort
• Dynamic programming
• Mathematic programming
  • Linear programming
• Search and enumeration Algorithms
  • Brute force algorithms
    • enumerating all possible candidate solutions and check
    • Improved brute force algorithms
      • e.g. branch and bound algorithms
    • Heuristic Algorithms
      • Local search
        • e.g Greedy search
      • Randomised Algorithms
        • Include Evolutionary Computation etc.

Heuristic Algorithms

• Heauristic: A (usually simple) algorithm that produces good enough solutions for a problem in a reasonable time frame
  • A Heuristic is a rule of thumb
  • Solutions are usually non-optimal but satisfactory
    • This makes them faster
    • Trade off is optimality or completeness
  • Usually used to solve high complexity problems
  • Includes deterministic e.g. local search and randomised algorithms

Randomised Algorithms

• Randomised Algorithm: An algorithm that uses a heuristic to make random choices during execution to produce a result.

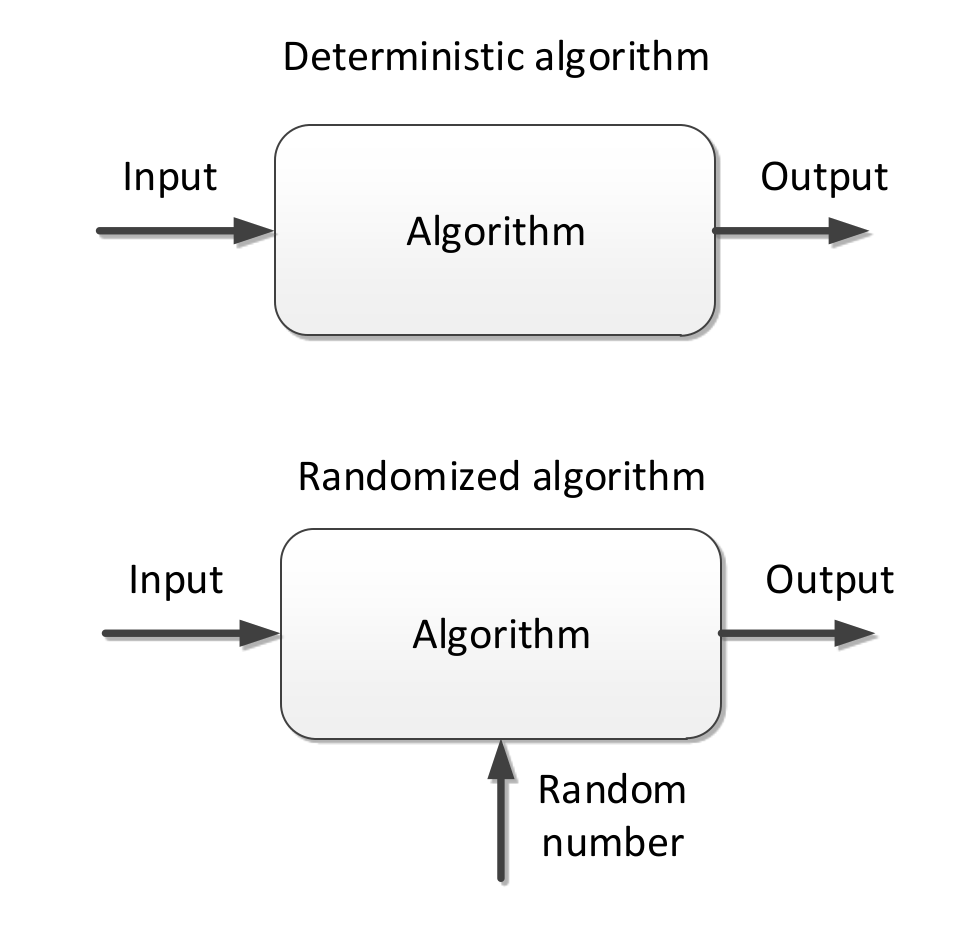
There are 2 categories of randomised algorithms:

1. Using random numbers to find a solution to a problem
2. Using random numbers to improve a solution to a problem

Category 1:

Las Vegas Algorithm

Problem: given an array of $n$ elements, find the first element which has a value equal to $x$

begin 
    repeat 
        Randomly select one element a out of n elements
    until a==x
end

Monte Carlo Algorithm

For the same problem we can also use the Monte Carlo algorithm

begin 
    i := 0
    repeat 
        Randomly select one element a out of n elements 
        i := i + 1 
    until (a==x) || (i==k)
end

Monte Carlo vs Las Vegas

The Las Vegas algorithm is a randomised algorithm that always gives correct results. The running time varies from run to run.

The Monte Carlo algorithm is also a randomised algorithm whose running time is deterministic but results may be incorrect with a small probability

Differences:

• Monte Carlo has a fixed numbers of steps
• Las Vegas algorithm runs in an infinite loop until the correct results are found
• Las Vegas algorithm can be converted into the Monte Carlo algorithm by using early termination.

Advantages of Randomised Algorithms

For a deterministic linear search algorithm, such as iterative search:

• The average run time complexity is $O( \frac{n+1}{2} \simeq O(n)$
• The worse case run time complexity is $O(n)$

For the Las Vegas algorithm:

• The average run time complexity is dependant on the input
• The worse time complexity is unbounded. i.e there are cases where the run time is relatively high

For the Monte Carlo algorithm:

• The run time for any situation is fixed as $O(1)$
• However, there is some probability of the wrong result being returned

Solving the Nuts and Bolts Problem using Randomised Algorithms

A disorganised carpenter has a collection of $n$ nuts of distinct sizes and $n$ bolts. They want to find the corresponding pairs of bolts and nuts.
Each nut matches exactly one bolt (and vice versa). They can only compare nuts to bolts (not nuts to nuts or bolts to bolts)

The brute force approach to solving this problem would be to compare each bolt to each nut with a time complexity of $O(n^2)$

We can use a quicksort approach to speedup the process.

Aside

The sorting problem: given and array $A$ of $n$ numbers, sort the numbers in increasing order.

Quicksort Algorithm:

less,equal, greater := three empty arrays
if length(array) > 1 {
  pivot := select an element of array
  for each x in array {
    if x < pivot add x to less
    if x = pivot add x to equal 
    if x > pivot add x to greater
  }
}
quicksort(less)
quicksort(greater)
array := concatenate(less,equal,greater)

Randomised Quicksort Algorithm

The time complexity of the deterministic quicksort algorithm is $O(n\log n)$ on average for a random permutation array

The worst case complexity is $O(n^2)$, this occurs when an already sorted array is entered

For the randomised quicksort algorithm: selecting a pivot point randomly

• Average run time complexity: $O(n\log n)$
• Worst case: $O(2n\log n) \simeq O(n\log n)$

Solving the problem using this apporach is not trivial and a proof can be found here

Applications of Randomised Algorithms

• Mathematics
  • Number theory
    • Primality test
    • Computational Geometry: graph algorithms
      • Minimum cut
• Computer Science
  • Data Analysis
    • PageRank
  • Parallel Computing
    • Deadlock avoidance
  • Optimisation
    • Nature inspired search and Search algorithms
• Computational Biology: DNA read alignment

Advantages and Disadvantages of Randomised Algorithms

Advantages

• Simplicity: usually easy to implement
• Performance: usually produce (near) optimum solutions with a high probability

Disadvantages

• Getting a wrong answer is a possibility
  • Can be solved by repeating the algorithm
• Difficult to analyse the running time and probability of getting an incorrect solution
• Impossible to be truly random