Lecture 4

• So far we have only looked at models with 1 parameter

(1)

$J(\Theta) = \mathbb{E}_{\mathcal{X,Y}\sim \mathcal{D}}-\log_{Pmodel}(\mathcal{Y | X; \Theta)}$

• We will nw look at models with many variables

Functions of multiple variables

Vectors

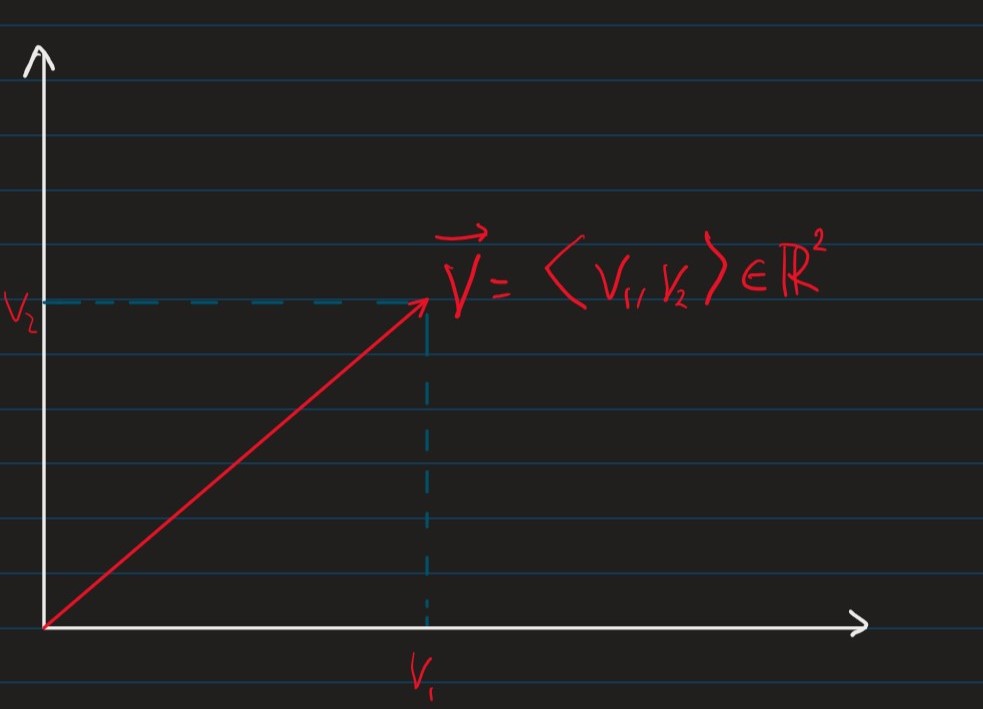
• Vectors are "arrays" of numbers e.g.

(2)

$\vec{v} = \langle v_1, \cdots, v_n \rangle \in \R^n$

• We can consider a vector as a point i a $n$ dimensional space where each point $v_i$ gives the coordinate along the $i^{th}$ axis.

Properties of vectors

• Norms: assigns "length" to vectors
• The $L^{p}$-norm of a vector $\vec{v}\in \R^n$ is

(3)

$\|\vec{v}\|_p = (\sum_{i=1}^{n}|v_i|^p)^{\frac{j}{p}}$

• The special case where $p=2$, $L^2$-norm is the euclidean norm/ distance denoted $\|\vec{v}\| = \|\vec{v}\|_2$

Operations on vectors

$\forall a \in \R, \\ \vec{u} \in \langle u_1, \cdots , u_m \rangle \in \R^m \\ \vec{v} \in \langle v_1, \cdots, v_m \rangle \in \R^m$

• $a \cdot \vec{u} = \langle au_1, \cdots, au_m \rangle \leftarrow$ Scalar Multiplication
• $\vec{v} + \vec{u} = \langle v_1 + u_1, \cdots , v_n+u_n \rangle \leftarrow$ Vector addition
• $\vec{v}\cdot\vec{u} = \sum_{i=1}^{m} v_iu_i \leftarrow$ Dot product

Theorem: Geometric interpretation of dot-product

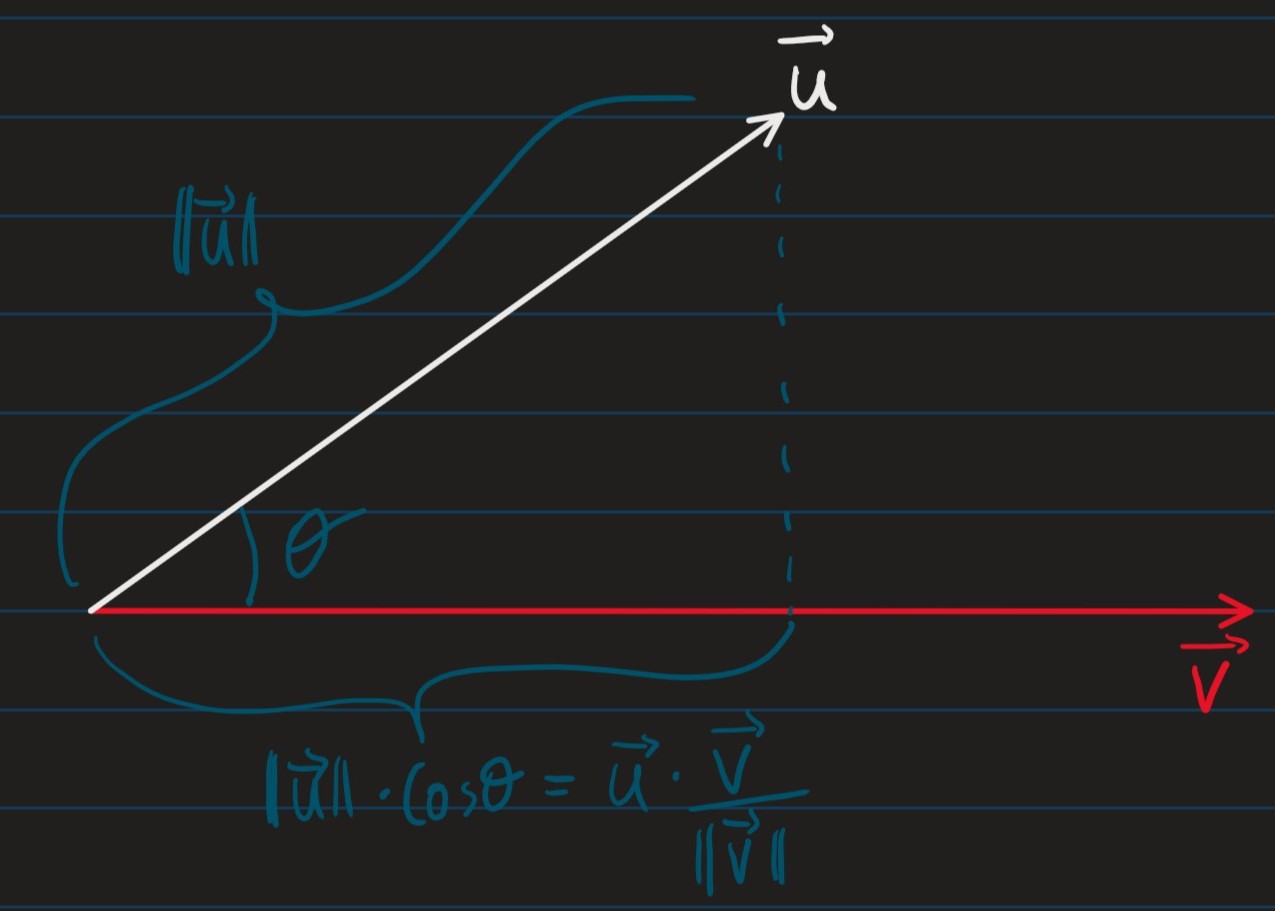
• Given the 2 vectors $\vec{u}, \vec{v}$, defined above, if the angle between them is $\theta$:

(4)

$\vec{u}\cdot\vec{v} = \|\vec{u}\| \cdot \|\vec{v}\|\cdot\cos\theta$

Partial Differentiation

• The partial derivative of the function $f(x_1,\cdots,x_n)$ in the direction of the variable $x_i$ at the point $\vec{u} = \langle u_1, \cdots, u_n \rangle$ is

(5)

$\frac{\delta f}{\delta x_i}(u_1,\cdots,u_n) = \lim_{h\rightarrow 0} \frac{f(u_1,\cdots,u_i+h,\cdots,u_n)-f(u_1,\cdots, u_n)}{h}$

Gradient

• The gradient of function $f(x_1,\cdots, x_n)$ is

(6)

$\nabla f := (\frac{\delta f}{\delta x_1},\cdots, \frac{\delta f}{\delta x_n})$

• And iff $f: \R^n \rightarrow \R$, then $\nabla f : \R^n \rightarrow \R^n$
  • i.e. the gradient is a vector-valued function

Chain Rule (Special Case)

For 1D functions	For higher dimensional functions
if $y=f(u)$ and $u = g(x)$ $\\$ then $\\$ $\frac{\delta y}{\delta x}= \frac{\delta y}{\delta u} \cdot \frac{\delta u}{\delta x}$	If $y=f(u_1,\cdots, u_m)$ and $u_i = g(x_1,\cdots,x_m)$ for $i \in \{1,\cdots,m\}$ $\\$ then $\\$ $\frac{\delta y}{\delta x_i} = \sum_{j=1}^m \frac{\delta y}{\delta u_j}\cdot \frac{\delta u_j}{\delta x_i}$

Directional Derivative

Definition

• Given a function:

(7)

$f : \R^m \rightarrow \R$

• And a vector

(8)

$\vec{v} = \langle v_1,\cdots,v_m\rangle \mid \|\vec{v}\| = 1$

• The directional derivative of $f$ at $\vec{x} = \langle x_1, \cdots, x_m \rangle$ along the vector $\vec{v}$ is

(9)

$\nabla_{\vec{v}} f(\vec{x}) := \lim_{\alpha \rightarrow 0} \frac{f(\vec{x}+ \alpha \vec{v}) - f(\vec{x})}{\alpha}$
$= \lim_{\alpha \rightarrow 0} \frac{f(x_1+ \alpha v_1 , \cdots, x_m + \alpha v_m)- f(x_1,\cdots, x_m)}{\alpha}$

Computing the Directional Derivative

• The following theorem implies that if we know the gradient $\nabla f$, then we can compute the derivative in any direction, $\vec{v}$

Theorem

(10)

$\nabla_{\vec{v}}f(x) = \nabla f(x)\cdot\vec{v}$

• Where:
  • $\nabla_{\vec{v}}f(x) \leftarrow$ is the directional derivative
  • $\nabla f(x) \leftarrow$ is the gradient

Proof

• Define the function

(11)

$h(\alpha) := f(u_1,\cdots,u_m)$

• Where:
  • $u_i := x_i + \alpha v_i, \forall i \in \{1,\cdots,m\}$
  • Note that $h : \R \rightarrow \R$, i.e. $h$ is a 1D real-valued function

(12)

$\nabla_{\vec{v}} f(\vec{x}) := \lim_{\alpha \rightarrow 0} \frac{f(\vec{x}+ \alpha \vec{v}) - f(\vec{x})}{\alpha}$

• From definition of $\nabla_{\vec{v}}f$

$=\lim_{\alpha\rightarrow 0} \frac{h(0+\alpha)=h(0)}{\alpha}$

• By definition of $g$

(13)

$= h'(0)$

• By definition of Derivative

• Using the Chain Rule, we have:

(14)

$h'(\alpha) = \frac{\delta h}{\delta \alpha} = \sum_{i=1}^m \frac{\delta u_i}{\delta \alpha} = \sum_{i=1}^m \frac{\delta f}{\delta u_i}\cdot v_i$

• Note that for $\alpha = 0$, we have:

(15)

$u_i = x_i + 0 \cdot v_i = x_i$

• Using (13), (14) and (15), we get:

(16)

$\nabla_{\vec{v}}f(\vec{x}) = h'(0) = \sum_{i=1}^m \frac{\delta f}{\delta x_i}\cdot v_i = \nabla f(x)\cdot \vec{v}$

The Gradient Points Towards the Steepest Ascent

• The vector $\vec{v}$ along which $f$ has steepest ascent is:

(17)

$\argmax_{\vec{v} , \|\vec{v}\|=1} \nabla_{\vec{v}}f(\vec{x})$

$= \argmax_{\vec{v} , \|\vec{v}\|=1} \nabla f(\vec{x}) \cdot \vec{v}$

$= \argmax_{\vec{v} , \|\vec{v}\|=1} \|\nabla f(\vec{x})\|\|\vec{v}\|\cdot \cos\theta$

$= \argmax_{\vec{v} , \|\vec{v}\|=1} \|\nabla f(\vec{x}) \|\cdot \cos\theta$

• Where $\cos\theta$ is the angle between $\vec{v}$ and $\nabla f(\vec{x})$

• $\implies$ The vector $\vec{v}$ which gives the steepest ascent is the vector that has angle $\theta=0$ to $\nabla f$, i.e. the vector $\vec{v}$ which points in the same direction as $\nabla f$

Method of Gradient Descent

Input: cost function: $J : \R^m \rightarrow \R$
           learning rate: $\epsilon \in \R, \epsilon > 0$

$\vec{x} \leftarrow$ Some initial point in $\R^m$
while termination condition not met {
             $\vec{x}\leftarrow \vec{x} - \epsilon \cdot \nabla J(\vec{x})$
}