- So far we have only looked at models with 1 parameter
J(Θ)=EX,Y∼D−logPmodel(Y∣X;Θ)
- We will nw look at models with many variables
- Vectors are "arrays" of numbers e.g.
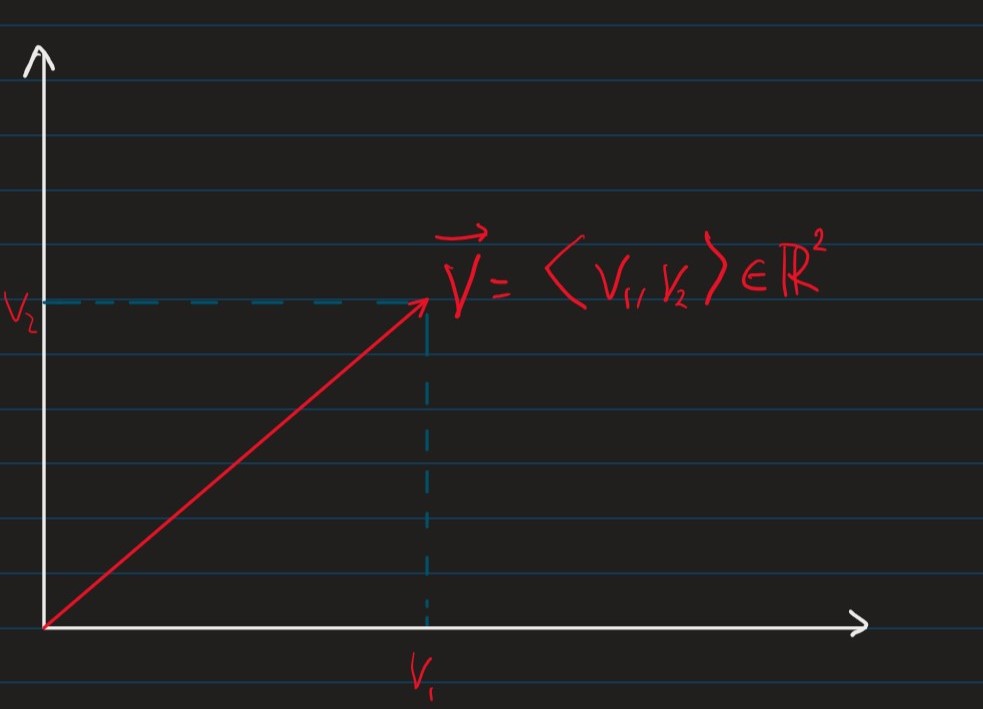
v=⟨v1,⋯,vn⟩∈Rn
- We can consider a vector as a point i a n dimensional space where each point vi gives the coordinate along the ith axis.
- Norms: assigns "length" to vectors
- The Lp-norm of a vector v∈Rn is
∥v∥p=(i=1∑n∣vi∣p)pj
- The special case where p=2, L2-norm is the euclidean norm/ distance denoted ∥v∥=∥v∥2
∀a∈R,u∈⟨u1,⋯,um⟩∈Rmv∈⟨v1,⋯,vm⟩∈Rm
- a⋅u=⟨au1,⋯,aum⟩← Scalar Multiplication
- v+u=⟨v1+u1,⋯,vn+un⟩← Vector addition
- v⋅u=∑i=1mviui← Dot product
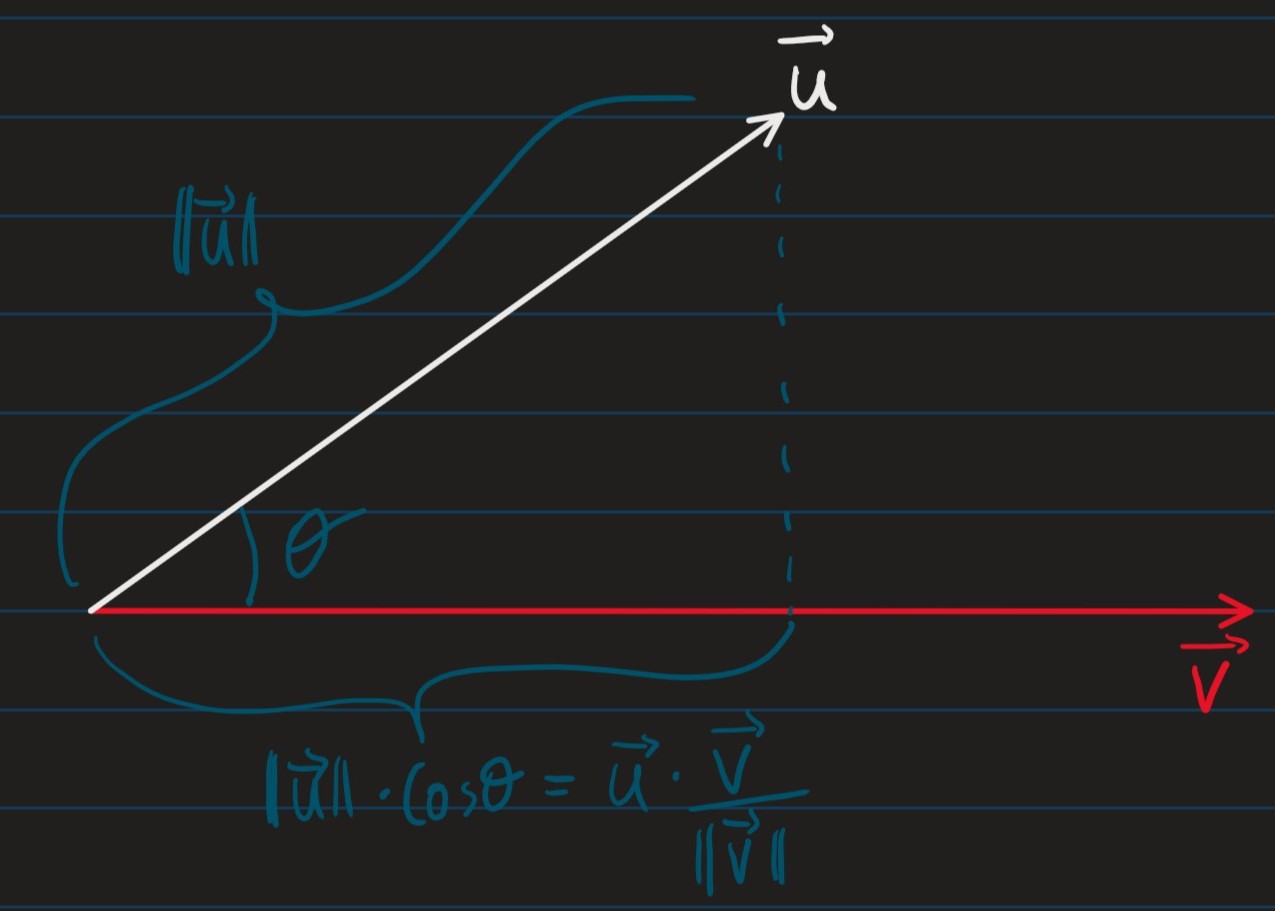
- Given the 2 vectors u,v, defined above, if the angle between them is θ:
u⋅v=∥u∥⋅∥v∥⋅cosθ
- The partial derivative of the function f(x1,⋯,xn) in the direction of the variable xi at the point u=⟨u1,⋯,un⟩ is
δxiδf(u1,⋯,un)=h→0limhf(u1,⋯,ui+h,⋯,un)−f(u1,⋯,un)
- The gradient of function f(x1,⋯,xn) is
∇f:=(δx1δf,⋯,δxnδf)
- And iff f:Rn→R, then ∇f:Rn→Rn
- i.e. the gradient is a vector-valued function
| For 1D functions |
For higher dimensional functions |
| if y=f(u) and u=g(x) then δxδy=δuδy⋅δxδu |
If y=f(u1,⋯,um) and ui=g(x1,⋯,xm) for i∈{1,⋯,m} then δxiδy=∑j=1mδujδy⋅δxiδuj |
f:Rm→R
v=⟨v1,⋯,vm⟩∣∥v∥=1
- The directional derivative of f at x=⟨x1,⋯,xm⟩ along the vector v is
∇vf(x):=α→0limαf(x+αv)−f(x)
=α→0limαf(x1+αv1,⋯,xm+αvm)−f(x1,⋯,xm)
- The following theorem implies that if we know the gradient ∇f, then we can compute the derivative in any direction, v
∇vf(x)=∇f(x)⋅v
- Where:
- ∇vf(x)← is the directional derivative
- ∇f(x)← is the gradient
h(α):=f(u1,⋯,um)
- Where:
- ui:=xi+αvi,∀i∈{1,⋯,m}
- Note that h:R→R, i.e. h is a 1D real-valued function
∇vf(x):=α→0limαf(x+αv)−f(x)
=α→0limαh(0+α)=h(0)
=h′(0)
h′(α)=δαδh=i=1∑mδαδui=i=1∑mδuiδf⋅vi
- Note that for α=0, we have:
ui=xi+0⋅vi=xi
∇vf(x)=h′(0)=i=1∑mδxiδf⋅vi=∇f(x)⋅v
- The vector v along which f has steepest ascent is:
v,∥v∥=1argmax∇vf(x)
=v,∥v∥=1argmax∇f(x)⋅v
=v,∥v∥=1argmax∥∇f(x)∥∥v∥⋅cosθ
=v,∥v∥=1argmax∥∇f(x)∥⋅cosθ
-
Where cosθ is the angle between v and ∇f(x)
-
⟹ The vector v which gives the steepest ascent is the vector that has angle θ=0 to ∇f, i.e. the vector v which points in the same direction as ∇f
Input: cost function: J:Rm→R
learning rate: ϵ∈R,ϵ>0
x← Some initial point in Rm
while termination condition not met {
x←x−ϵ⋅∇J(x)
}

