We will describe ML models using computation graphs where
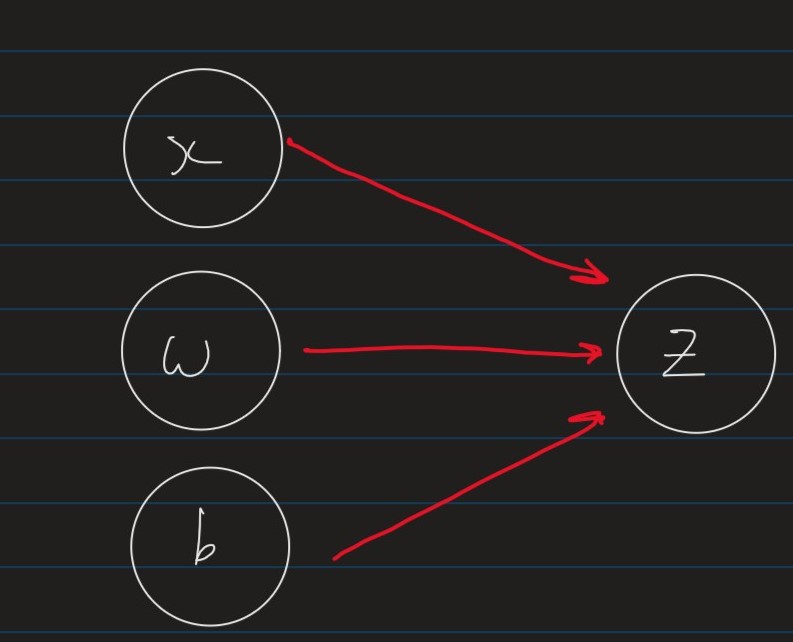
Nodes represent variables (values, vectors, matrices)Edges represent functional dependencies
i.e. an edge from x x x y y y y y y x x x
The linear regression model, z = ∑ i = 1 m a i w i + b z = \sum_{i=1}^m a_iw_i+b z = ∑ i = 1 m a i w i + b
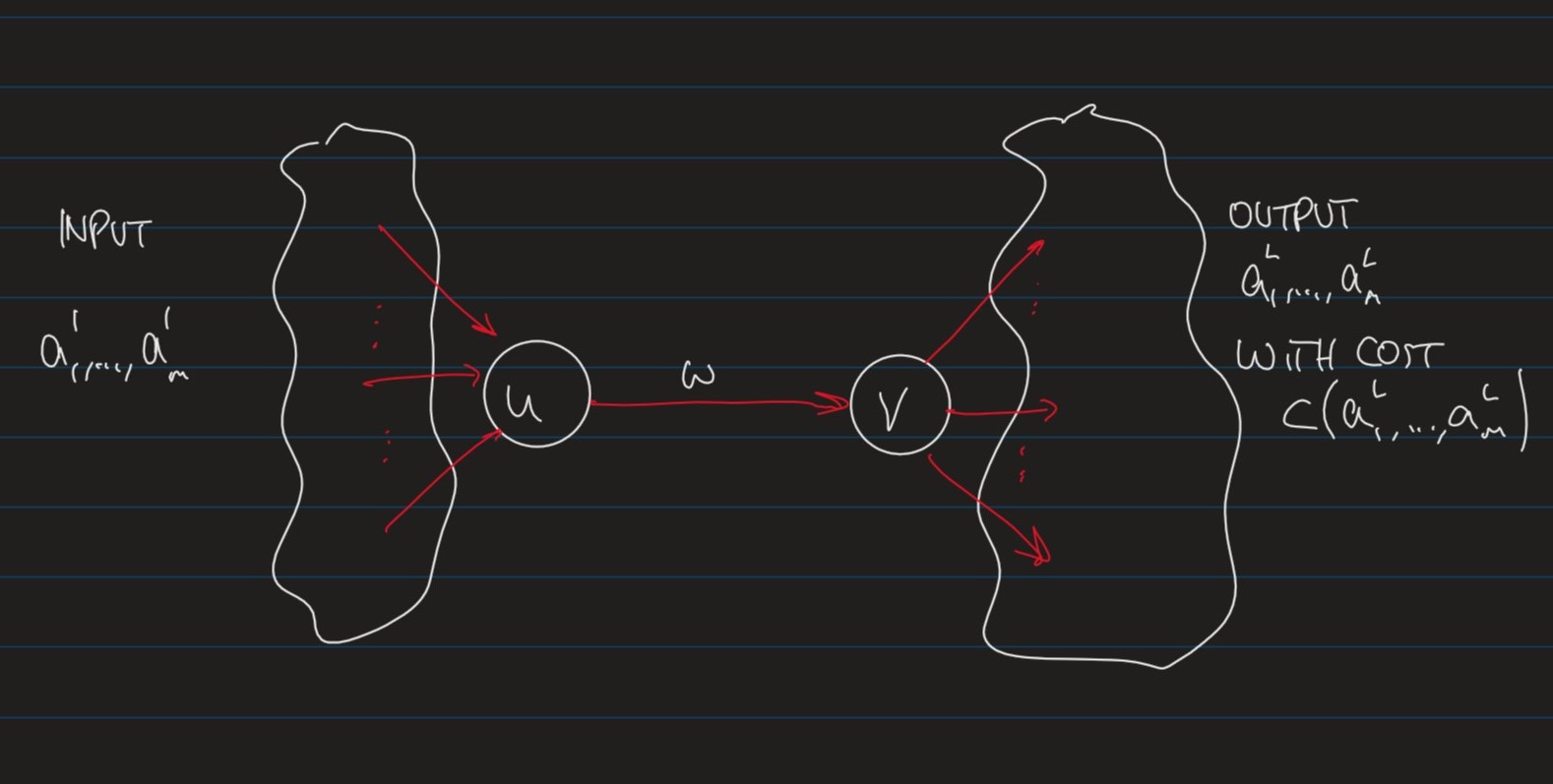
Stepping it up, here is a simple Feed-forward Neural Network:
Where:
L ← L \leftarrow L ←
layer 1 is the "input layer"
layer L L L "output layer"
m ← m\leftarrow m ← "width" of the network, which can change for each layerw j k l ← w_{jk}^l\leftarrow w j k l ← "weight" of the connection between the k t h k^{th} k t h l − 1 l-1 l − 1 j t h j^{th} j t h l l l b j l ← b_j^l\leftarrow b j l ← "bias" of the j t h j^{th} j t h l l l
Note: These appear for every z z z
z j l = ∑ k w j k l a k l − 1 + b j l ← z_j^l = \sum_k w_{jk}^l a_k^{l-1} + b_j^l \leftarrow z j l = ∑ k w j k l a k l − 1 + b j l ← j j j l l l a j l = ϕ ( z j l ) ← a_j^l = \phi(z_j^l)\leftarrow a j l = ϕ ( z j l ) ← "activation" of unit j j j l l l ϕ \phi ϕ "activation function" .
The parameters of the network are:
The weights w j k l w_{jk}^l w j k l
The Biases b j l b_j^l b j l
To apply gradient descent to optimise a weight w w w b b b
δ C δ w = δ C δ v ⋅ δ v δ w \frac{\delta C}{\delta w} = \frac{\delta C}{\delta v}\cdot\frac{\delta v}{\delta w} δ w δ C = δ v δ C ⋅ δ w δ v
z j l = ∑ k = 1 m w j k l a k l − 1 + b j l z_j^l = \sum_{k=1}^m w_{jk}^l a_k^{l-1}+ b_j^l z j l = k = 1 ∑ m w j k l a k l − 1 + b j l
a j l = ϕ ( z j l ) a_j^l = \phi(z_j^l) a j l = ϕ ( z j l )
δ C δ w j k l = δ C δ z j l ⋅ δ z j l δ w j k l = δ C δ z j l ⋅ a k l − 1 \frac{\delta C}{\delta w_{jk}^l} = \frac{\delta C}{\delta z_j^l}\cdot\frac{\delta z_j^l}{\delta w_{jk}^l} = \frac{\delta C}{\delta z_j^l}\cdot a_k^{l-1} δ w j k l δ C = δ z j l δ C ⋅ δ w j k l δ z j l = δ z j l δ C ⋅ a k l − 1
Where a k l − 1 a_k^{l-1} a k l − 1 "activation" of unit k k k l − 1 l-1 l − 1
δ C δ b j l = δ C δ z j l ⋅ δ z j l δ b j l = δ C δ z j l ⋅ 1 \frac{\delta C}{\delta b_j^l} = \frac{\delta C}{\delta z_j^l}\cdot \frac{\delta z_j^l}{\delta b_j^l} = \frac{\delta C}{\delta z_j^l}\cdot 1 δ b j l δ C = δ z j l δ C ⋅ δ b j l δ z j l = δ z j l δ C ⋅ 1
Hence, we can compute δ C δ w k j \frac{\delta C}{\delta w_{kj}} δ w k j δ C δ C δ b j l \frac{\delta C}{\delta b_j^l} δ b j l δ C
δ j l : = δ C δ z j l \delta_j^l := \frac{\delta C}{\delta z_j^l} δ j l : = δ z j l δ C
The vector δ l \delta^l δ l local gradient for layer l l l
a j L = ϕ ( z j L ) a_j^L = \phi(z_j^L) a j L = ϕ ( z j L )
The local gradient for the output layer is:
δ j L = δ C δ z j L \delta_j^L = \frac{\delta C}{\delta z_j^L} δ j L = δ z j L δ C By definition
= δ C δ a j L ⋅ δ a j L δ z j L = \frac{\delta C}{\delta a_j^L}\cdot\frac{\delta a_j^L}{\delta z_j^L} = δ a j L δ C ⋅ δ z j L δ a j L
= δ C δ a j L ⋅ ϕ ′ ( z j L ) = \frac{\delta C }{\delta a_j^L} \cdot \phi'(z_j^L) = δ a j L δ C ⋅ ϕ ′ ( z j L ) a j L = ϕ ( z j L ) a_j^L = \phi(z_j^L) a j L = ϕ ( z j L )
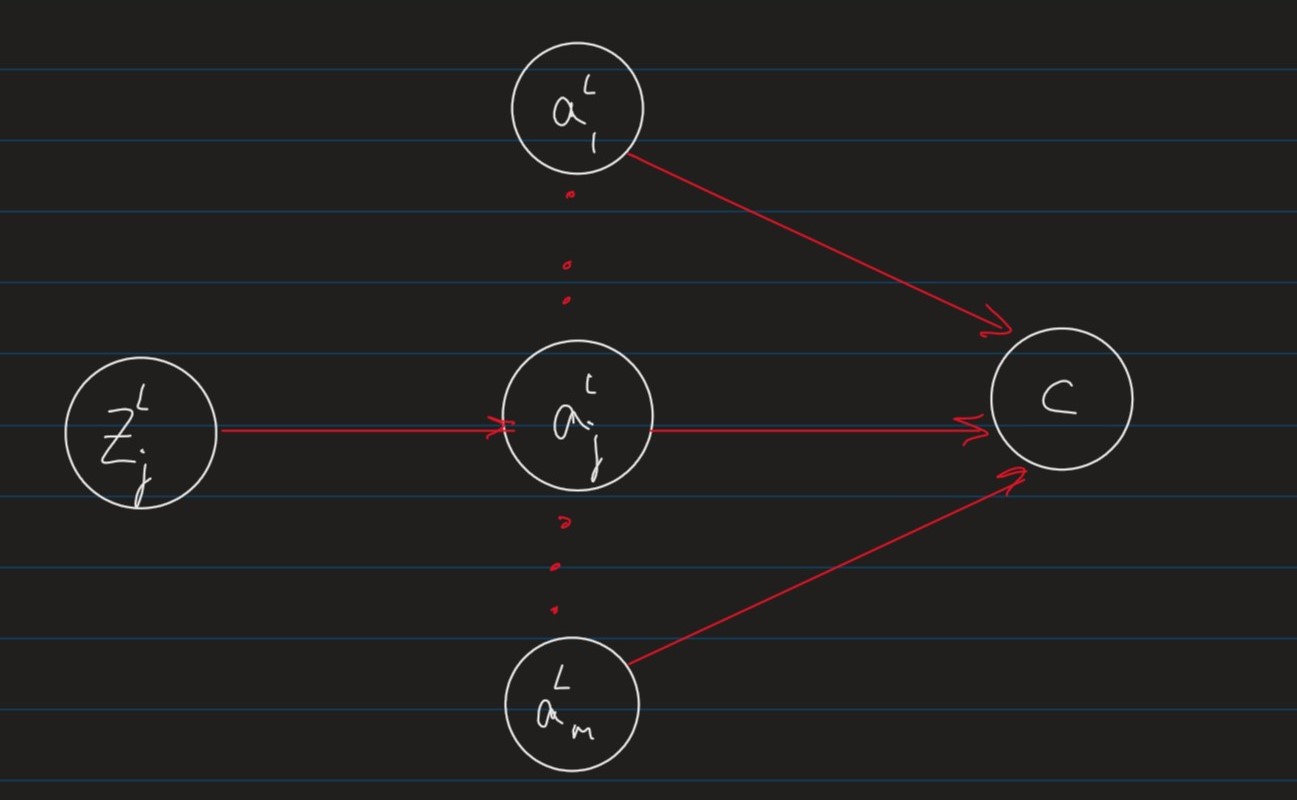
The partial derivative δ C δ a j L \frac{\delta C}{\delta a_j^L} δ a j L δ C m m m
C ( a 1 L , ⋯ , a m L ) : = 1 2 ∑ k = 1 m ( y k − a k L ) 2 C(a_1^L,\cdots,a_m^L) := \frac{1}{2}\sum_{k=1}^m (y_k - a_k^L)^2 C ( a 1 L , ⋯ , a m L ) : = 2 1 k = 1 ∑ m ( y k − a k L ) 2
y k y_k y k k t h k^{th} k t h
a k L a_k^L a k L k t h k_{th} k t h
i.e. this is essentially mean squared error
in which case,
δ C δ a j L = a j L − y j \frac{\delta C}{\delta a_j^L}= a_j^L - y_j δ a j L δ C = a j L − y j
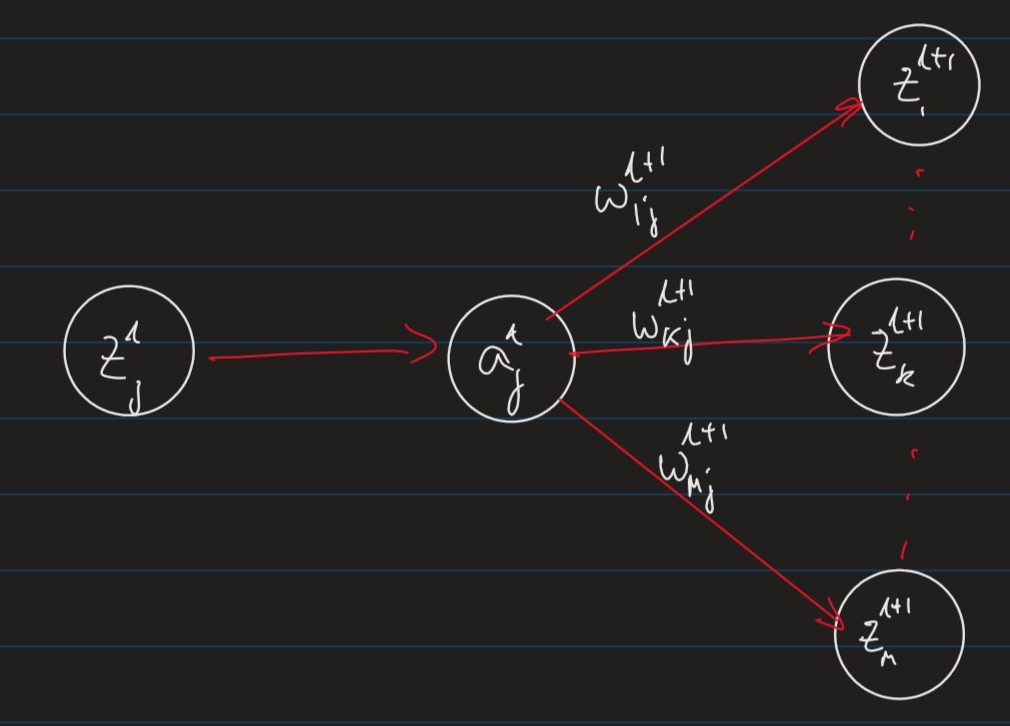
z k l + 1 = ∑ r w k r l + 1 a r l z_k^{l+1} = \sum_r w_{kr}^{l+1} a_r^l z k l + 1 = r ∑ w k r l + 1 a r l
a j l = ϕ ( z j l ) a_j^l = \phi(z_j^l) a j l = ϕ ( z j l )
δ j l = δ C δ z j l \delta_j^l = \frac{\delta C}{\delta z_j^l} δ j l = δ z j l δ C definition of local gradient δ j l \delta_j^l δ j l = δ C δ a j l ⋅ δ a j l δ z j l = \frac{\delta C}{\delta a_j^l}\cdot \frac{\delta a_j^l}{\delta z_j^l} = δ a j l δ C ⋅ δ z j l δ a j l = ( ∑ k δ C δ z k l + 1 ⋅ δ z k l + 1 δ a j l ) ⋅ ϕ ′ ( z j l ) = \left(\sum_k \frac{\delta C}{\delta z_k^{l+1}} \cdot \frac{\delta z_k^{l+1}}{\delta a_j^l}\right)\cdot \phi'(z_j^l) = ( k ∑ δ z k l + 1 δ C ⋅ δ a j l δ z k l + 1 ) ⋅ ϕ ′ ( z j l ) δ C δ a j l \frac{\delta C}{\delta a_j^l} δ a j l δ C
= ϕ ′ ( z j l ) ∑ k δ k l + 1 ⋅ w k j l + 1 = \phi'(z_j^l)\sum_k \delta_k^{l+1}\cdot w_{kj}^{l+1} = ϕ ′ ( z j l ) k ∑ δ k l + 1 ⋅ w k j l + 1 definition of local gradient δ k l + 1 \delta_k^{l+1} δ k l + 1
∀ \forall ∀ w w w b b b
δ C δ w j k l = δ j l ⋅ a k l − 1 \frac{\delta C}{\delta w_{jk}^l} = \delta_j^l\cdot a_k^{l-1} δ w j k l δ C = δ j l ⋅ a k l − 1
δ C δ b j l = δ j l \frac{\delta C}{\delta b_j^l} = \delta_j^l δ b j l δ C = δ j l
Where the local gradient δ j l \delta_j^l δ j l
δ j l = { ϕ ′ ( z j L ) ⋅ δ C δ a j L if l = L (output layer) ϕ ′ ( z j l ) ⋅ ∑ k δ k l + 1 ⋅ w k j l + 1 otherwise (hidden layer) \delta_j^l =
\begin{cases}
\phi'(z_j^L)\cdot \frac{\delta C}{\delta a_j^L} &\text{if $l=L$ (output layer)} \\\\
\phi'(z_j^l)\cdot\sum_k \delta_k^{l+1}\cdot w_{kj}^{l+1} &\text{otherwise (hidden layer)}
\end{cases} δ j l = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ϕ ′ ( z j L ) ⋅ δ a j L δ C ϕ ′ ( z j l ) ⋅ ∑ k δ k l + 1 ⋅ w k j l + 1 if l = L (output layer) otherwise (hidden layer)
The back-propagation algorithm can exploit efficient implementations of matrix operations
Note: recall that for a matrix A ∈ R m × R n \textbf{A} \in \R^m\times\R^n A ∈ R m × R n A i j A_ij A i j i t h i^{th} i t h j t h j^{th} j t h
For two matrices A ∈ R m × R n \textbf{A} \in \R^m\times\R^n A ∈ R m × R n B ∈ R n × R l \textbf{B} \in \R^n\times\R^l B ∈ R n × R l
Operation
Name
( A T ) i j = A j i (\textbf{A}^T)_{ij} = A_{ji} ( A T ) i j = A j i Matrix Transpose
( AB ) i j = ∑ k A i k B k j (\textbf{AB})_{ij} = \sum_k \textbf{A}_{ik}\textbf{B}_{kj} ( AB ) i j = ∑ k A i k B k j Matrix Multiplication
For two vectors u ⃗ , v ⃗ ∈ R m \vec{u},\vec{v} \in \R^m u , v ∈ R m
Operation
Name
u ⃗ + v ⃗ = ⟨ u 1 + v 1 , ⋯ , u m + v m ⟩ \vec{u}+\vec{v} = \langle u_1+v_1,\cdots,u_m+v_m\rangle u + v = ⟨ u 1 + v 1 , ⋯ , u m + v m ⟩ Vector addition
u ⃗ ⋅ v ⃗ = ∑ i = 1 m u i v i \vec{u}\cdot\vec{v} = \sum_{i=1}^m u_iv_i u ⋅ v = ∑ i = 1 m u i v i Dot Product
u ⃗ ⊙ u ⃗ = ⟨ u 1 v 1 , ⋯ , u m v m ⟩ \vec{u}\odot\vec{u} = \langle u_1v_1,\cdots,u_mv_m \rangle u ⊙ u = ⟨ u 1 v 1 , ⋯ , u m v m ⟩ Hadamard Product
( u ⃗ v ⃗ T ) i j = u i v j (\vec{u}\vec{v}^T)_{ij} = u_iv_j ( u v T ) i j = u i v j Outer Product
z l = ( z 1 l , ⋯ , z m l ) z^l = (z_1^l, \cdots, z_m^l) z l = ( z 1 l , ⋯ , z m l )
= ( ∑ k = 1 m w 1 k l a k l − 1 + b 1 l , ⋯ , ∑ k = 1 m w m k l a k l − 1 + b m l ) = \left( \sum_{k=1}^m w_{1k}^la_k^{l-1} + b_1^l, \cdots, \sum_{k=1}^m w_{mk}^la_k^{l-1}+ b_m^l \right) = ( k = 1 ∑ m w 1 k l a k l − 1 + b 1 l , ⋯ , k = 1 ∑ m w m k l a k l − 1 + b m l )
= w l a l − 1 + b = w^la^l-1 + b = w l a l − 1 + b
a l = ( a 1 l , ⋯ , a m l ) a^l = (a_1^l,\cdots, a_m^l) a l = ( a 1 l , ⋯ , a m l )
= ( ϕ ( z 1 l ) , ⋯ , ϕ ( z m l ) ) = (\phi(z_1^l), \cdots, \phi(z_m^l)) = ( ϕ ( z 1 l ) , ⋯ , ϕ ( z m l ) )
= ϕ ( z l ) =\phi(z^l) = ϕ ( z l )
δ L = ( δ 1 L , ⋯ , δ m L ) \delta^L = (\delta_1^L,\cdots, \delta_m^L) δ L = ( δ 1 L , ⋯ , δ m L )
= ( δ C δ a 1 L ⋅ ϕ ′ ( z 1 L ) , ⋯ , δ C δ a m L ⋅ ϕ ′ ( z m L ) ) = \left( \frac{\delta C}{\delta a_1^L}\cdot \phi'(z_1^L), \cdots, \frac{\delta C}{\delta a_m^L}\cdot\phi'(z_m^L) \right) = ( δ a 1 L δ C ⋅ ϕ ′ ( z 1 L ) , ⋯ , δ a m L δ C ⋅ ϕ ′ ( z m L ) )
= ∇ a L C ⊙ ϕ ′ ( z L ) = \nabla_{a^L}C \odot \phi'(z^L) = ∇ a L C ⊙ ϕ ′ ( z L )
δ l = ( δ 1 l , ⋯ , δ m l ) \delta^l = (\delta_1^l, \cdots, \delta_m^l) δ l = ( δ 1 l , ⋯ , δ m l )
= ( ϕ ′ ( z 1 l ) ⋅ ∑ k δ k l + 1 ⋅ w k 1 l + 1 , ⋯ , ϕ ′ ( z m l ) ⋅ ∑ k δ k l + 1 ⋅ w k m l + 1 ) = \left( \phi'(z_1^l)\cdot\sum_k \delta_k^{l+1}\cdot w_{k1}^{l+1} , \cdots, \phi'(z_m^l)\cdot \sum_k \delta_k^{l+1}\cdot w_{km}^{l+1}\right) = ( ϕ ′ ( z 1 l ) ⋅ k ∑ δ k l + 1 ⋅ w k 1 l + 1 , ⋯ , ϕ ′ ( z m l ) ⋅ k ∑ δ k l + 1 ⋅ w k m l + 1 )
= ϕ ′ ( z l ) ⊙ ( ∑ k ( w l + 1 ) 1 k T δ k l + 1 , ⋯ , ∑ k ( w l + 1 ) m k T δ k l + 1 ) = \phi'(z^l) \odot \left( \sum_k (w^{l+1})_{1k}^T\delta_k^{l+1},\cdots, \sum_k(w^{l+1})_{mk}^T\delta_k^{l+1}\right) = ϕ ′ ( z l ) ⊙ ( k ∑ ( w l + 1 ) 1 k T δ k l + 1 , ⋯ , k ∑ ( w l + 1 ) m k T δ k l + 1 )
= ϕ ′ ( z l ) ⊙ ( w l + 1 ) T δ l + 1 = \phi'(z^l)\odot (w^{l+1})^T\delta^{l+1} = ϕ ′ ( z l ) ⊙ ( w l + 1 ) T δ l + 1
Input : A training example, ( x , y ) ∈ R m × R m ′ (x,y)\in \R^m\times\R^{m'} ( x , y ) ∈ R m × R m ′
Set the activation in the input layera 1 = x a^1 = x a 1 = x
for each l = ( 2 ⋯ L ) l=(2\cdots L) l = ( 2 ⋯ L ) z l = w l a l − 1 + b l z^l = w^la^{l-1}+b^l z l = w l a l − 1 + b l a l = ϕ ( z l ) a^l = \phi(z^l) a l = ϕ ( z l )
Compute local gradient for output layerδ L : = ∇ a L C ⊙ ϕ ′ ( z L ) \delta^L := \nabla_{a^L}C \odot \phi'(z^L) δ L : = ∇ a L C ⊙ ϕ ′ ( z L )
Backpropagate local gradients for hidden layers, i.el = ( L − 1 ⋯ 2 ) l=(L-1 \cdots 2) l = ( L − 1 ⋯ 2 ) δ l : = ( ( w l + 1 ) T δ l + 1 ) ⊙ ϕ ′ ( z l ) \hspace{10px}\delta^l := \left( (w^{l+1})^T\delta^{l+1}\right)\odot \phi'(z^l) δ l : = ( ( w l + 1 ) T δ l + 1 ) ⊙ ϕ ′ ( z l )
return the partial derivatioesδ C δ w j k l = a k l − 1 δ j l \frac{\delta C}{\delta w_{jk}^l} = a_k^{l-1}\delta_j^l δ w j k l δ C = a k l − 1 δ j l δ C δ b j l = δ j l \frac{\delta C}{\delta b_j^l} = \delta_j^l δ b j l δ C = δ j l
Assume n n n
( x 1 , y 1 ) , ⋯ , ( x n , y n ) (x_1,y_1),\cdots,(x_n,y_n) ( x 1 , y 1 ) , ⋯ , ( x n , y n )
and a cost function:
C = 1 m ∑ i = 1 n C i C = \frac{1}{m}\sum_{i=1}^n C_i C = m 1 i = 1 ∑ n C i
Where C i C_i C i i t h i^{th} i t h
For example, with Mean Squared error, we can define it as:
C i = 1 2 ( y i − a L ) C_i = \frac{1}{2}(y_i-a^L) C i = 2 1 ( y i − a L )
Where a L a^L a L a 1 = x i a^1 = x_i a 1 = x i
Backpropagation gives us the gradient of the overall cost function as follows:
δ C δ w l = 1 m ∑ i = 1 n δ C i δ w l \frac{\delta C}{\delta w^l} = \frac{1}{m}\sum_{i=1}^n \frac{\delta C_i}{\delta w^l} δ w l δ C = m 1 i = 1 ∑ n δ w l δ C i
δ C δ b l = 1 m ∑ i = 1 n δ C i δ B l \frac{\delta C}{\delta b^l} = \frac{1}{m}\sum_{i=1}^n \frac{\delta C_i}{\delta B^l} δ b l δ C = m 1 i = 1 ∑ n δ B l δ C i
Note: these provide the average gradient per training example
We can now use gradient descent to optimise the weights, w w w b b b
Computing the gradients is expensive when the number of training examples, n n n
We can approximate the gradients:
δ C δ w l ≈ 1 b ∑ i = 1 b δ C i δ w l \frac{\delta C}{\delta w^l} \approx \frac{1}{b}\sum_{i=1}^b \frac{\delta C_i}{\delta w^l} δ w l δ C ≈ b 1 i = 1 ∑ b δ w l δ C i
δ C δ b l ≈ 1 b ∑ i = 1 b δ C i δ b l \frac{\delta C}{\delta b^l} \approx \frac{1}{b} \sum_{i=1}^b \frac{\delta C_i}{\delta b^l} δ b l δ C ≈ b 1 i = 1 ∑ b δ b l δ C i
using a random "mini-batch" of b ≤ n b\leq n b ≤ n
Size
Name
1 < b < n 1<b<n 1 < b < n Mini-batch Gradient Descent
b = 1 b=1 b = 1 Stochastic Gradient Descent
b = n b=n b = n Batch Gradient Descent
It is common to use mini-batch size of b ∈ ( 20 , 100 ) b \in (20,100) b ∈ ( 2 0 , 1 0 0 )