Lecture 5

Mutual Exclusion

Events

• An event $a_0$ of thread $A$ is
  • Instantaneous
    • Even if two events attempt to execute at exactly the same moment in time, one will execute before the other.
  • Has no simultaneous events

• A thread $A$ is a sequence, $(a_0,\cdots)$ of events
  • $a_0 \prec a_1$ indicates order or precedence

• Thread events include the following:

  • Assign to shared variable
  • Assign to local variable
  • Method invocation
  • Method return

• Essentially every low level operation is a thread event.

• Threads can be represented as state machines/ finite state automata

  • Thread State
    • Program counter
    • (Thread) Local variables
  • System State
    • Shared variables
    • Union of thread states

Concurrency

• Two or more threads executing at the same time.
• Their execution is interleaved on the timeline
• They are not necessarily independent as they may be interacting during the course of execution.

Where yellow shows events from thread $A$ and green shows events from thread $B$

Intervals

• An interval $A_0 = (a_0,a_1)$ represents the time between events $a_0$ and $a_1$

• Intervals may overlap or be disjoint.

  • In critial sections we want them to be disjoint.

• We can define precedence of intervals as

  • $A_0 \prec B_0$ iff
    • The end of event $A_0$ is before the start of event $B_0$

Precedence Ordering

• A precedence order is a partial order

• Partial orders have the following properties:

  • Irreflexive
    • Never true that $A\prec A$
  • Antisymmetric
    • $A\prec B \implies B \nprec A$
  • Transitive
    • $(A \prec B) \cap (B \prec C) \implies A \prec C$

• Interestingly, $A\prec B$ and $B \prec A$ can both be false, this is what makes it a partial order

• Total orders on the other hand are:

  • Irreflexive
  • Antisymmetric
  • Transitive
  • Except that $\forall A,B, A\neq B, (A\prec B) \cup (B \prec A)$ Trichotomy

Repeated events

while (mumble){
    a_0 ; a_1
}

Here we have to distinguish between each run of the same events
i.e. $a_0^k$ representing the $k^{th}$ occurrence of event $a_0$ and $A_0^k$ is the $k^{th}$ occurrence of interval $A_0 = (a_0,a_1)$

We make variables indivisible using locks, i.e. able to withstand attempted concurrent accesses.

Locks

In Java, we can use the Lock interface

public interface Lock {

    public void lock();

    public void unlock();
}

public class Counter {
    private long value;
    private Lock lock;
    public long getAndIncrement() {
        lock.lock();
        try{
            value ++;
        }finally{
            lock.unlock();
        }
        return temp;
    }
}

Desired Properties of Locks

Mutual Exclusion:

• Let $CS_i^k$ be the thread $i$'s $k^{th}$ critical section execution
• Let $CS_j^m$ be $j$'s $m^{th}$ execution
• Then either $CS_i^K \prec CS_j^m$ or $CS_j^m \prec CS_i^k$

Deadlock Free:

• If any thread calls lock() then some thread will acquire it.
• If some thread calls lock()
  • And never returns
  • then other threads must be completing lock() and unlock() calls infinitely often.
• System as a whole makes progress
  • even if individuals starve

Starvation Free:

• If some thread calls lock()
  • it will eventually return
• Individual threads make progress

LockOne, for 2 threads

Note: $i$ is the current thread and $j$ is the other thread

class LockOne implements Lock {
    private boolean[] flag = new boolean[2]
    public void lock(){
        int i = ThreadID.get();
        int j = 1-i;
        flag[i] = true;
        while (flag[j]) {/*wait*/}
    }
    public void unlock(){
        int i = ThreadID.get();
        flag[i] = false;
    }
}

Proof LockOne Satisfies Mutual Exclusion

• Assume $CS_A^j$ overlaps with $CS_B^k$
• Consider each thread's last read and write in the lock() method before entering the critical section.

From the code:

$write_A(flag[A]=true)^{[6]} \prec read_A(flag[B]==false)^{[7]} \prec CS_A$

$write_B(flag[B]=true)^{[2]} \prec read_B(flag[A]==false)^{[3]} \prec CS_B$

From our assumption:

$read_A(flag[B]==false)^{[8]} \prec write_B(flag[B]=true)^{[1]}$

$read_B(flag[A]==false)^{[4]} \prec write_A(flag[A]=true)^{[5]}$

We can then see a cycle form between $[1],[2],[3],[4],[5], [6], [7] \text{and} [8]$, therefore such a series of events is impossible due to it being a partial order.

Proof LockOne Satisfies Deadlock Freedom

• LockOne fails deadlock freedom as concurrent execution can deadlock.
• i.e. if both threads attempt access at the same time, both of the following occur:

flag[i] = true;
while(flag[j]){}

flag[j] = true;
while(flag[i]){}

LockTwo for 2 threads

public class LockTwo implements Lock { 
    private int victim; 
    public void lock() {
        victim = i;
        while (victim == i){/* wait */}
    }
    public void unlock(){}
}

• This lock works by allowing another thread to go before it, eventually another thread gives it permission to go and begins to wait itself.

• LockTwo satisfies mutual exclusion

  • if thread $i$ is in the CS then the victim = $j$, due to boolean cannot be both 0 and 1.

• It is not deadlock free

  • sequential execution deadlocks
    • i.e. no other thread tries to get the lock, the waiting thread is never released
  • Concurrent execution does not.

Peterson's Algorithm

public void lock(){
    flag[i] = true;
    victim = i;
    while (flag[j] && victim == i){/* wait */}
}
public void unlock(){
    flag[i] = false;
}

• In this lock the flag variable is used to signify interest in entering the CS.
• The victim again is used to defer access to another thread.
• The thread then waits while it is both interested and the victim
• To unlock the thread just removes the sign of interest

Mutual Exclusion for Peterson's Algorithm

From the code:

(1)

$write_B(flag[B]=true) \prec write_B(victim=B)$

(2)

$write_A(victim=A) \prec read_A(flag[B]) \prec read_A(victim)$

Assumption:

(3)

$write_B(victim=B)\prec write_A(victim=A)$

• Assume thread $A$ is the last thread to write to victim

Combining these results in [1] $\rightarrow$ [3] $\rightarrow$ [2]

• From the end of [2] you can see that if $A$ reds flag[B] == true and victim==A then it could not have entered the critical section. quod erat demonstrandum

Deadlock Freedom for Peterson's Lock

• Thread blocked
  • only at while loop
  • only if other thread's flag is true
  • only if it is the victim

Starvation Freedom for Peterson's Lock

• Thread $i$ blocked only if $j$ repeatedly re-enters so that flag[j] == true && victim=1
• When $j$ re-enters, it sets the victim to $j$ so $i$ enters

All of these proofs have only been for 2 threads, what about the $n$ thread case?

Filter Algorithm for $n$ Threads

• There are $n-1$ waiting rooms called levels
• At each level
  • at least one thread enters
  • at least one thread is blocked at that level if many try to move to the next
• Only one thread makes it through a level at a time
• A thread at level $j$ is also at level $j-1,\cdots,0$

class Filter implements Lock{
    int[] level;
    int[] victim;

    public Filter(int n){
        level = new int[n];
        victim = new int[n];
        for (int i = 1; i<n; i++){
            level[i] = 0;
        }
    } 
    
    public void lock(){
        for (int L = 1; L < n; L++){
            level[i] = L;
            victim[L] = i;
            while (there is a thread at the same or a higher level and I am the victim){/*wait*/}
        }
    }
    public void unlock(){
        level[i] = 0;
    }
}

Claim of Filter Algorithm

• If you start at level $L=0$
• At most $n-L$ threads enter $L$
• Mutual exclusion at level $L=n-1$

Induction Hypothesis

• No more than $n-(L-1)$ threads at level $L-1$
• Induction step: by contradition
  • Assume all at level $L-1$ enter level $L$
  • $A$ is last to write victim[L]
  • $B$ is any other thread at level $L$
• Show that $A$ must have seen $B$ in level[L] and since victim[L] == A, it could not have entered

From the code:

(4)

$write_B(level[B]=L) \prec write_B(victim[L]=B)$

(5)

$write_A(victim[L]=A) \prec read_A(level[B]) \prec read_A(victim[L])$

By assumption that thread $A$ is last to write victim[L]:

(6)

$write_B(victim[L]=B) \prec write_A(victim[L]=A)$

• Combining these yields: [4] $\rightarrow$ [6] $\rightarrow$ [7]
• $A$ read level[B] >= L and victim[L]=A therefore, A could not have entered $L$

Filter Starvation Free

• Filter lock satisfies this property just as Peterson does
• However, it is not very fair as threads can be overtaken by others

Bounded Waiting

• We want to enforce stronger fairness guarantees

• Thread not overtaken too often

• if $A$ starts before $B$, then $A$ should enter the CS before $B$

  • What does start mean?

• Divide lock() method into 2 parts

  • Doorway interval
    • Denoted $D_A$
    • Always finished in a finite number of steps
  • Waiting interval
    • Denoted $W_A$
    • May take unbounded number of steps

First-Come-First-Served

• For threads $A$ and $B$:
  • if $D_A^k \prec D_B^j$
    • $A$'s $k^{th}$ doorway precedes $B$'s $j^{th}$ doorway
  • Then, $CS_A^k \prec CS_B^j$
    • $A$'s $k^{th}$ critical section precedes $B$'s $j^{th}$ critical section
    • $B$ cannot overtake $A$

Fairness of Filter Lock

• The Filter Lock satisfies properties:
  • No one starves
  • But very weak fairness
    • a waiting thread can be overtaken an arbitrary number of times

Bakery Algorithm

• Provides fairness via the First-Come-First-Served topology
• It does this by assigning each waiting thread a number and the current lowest waiting number is served next
• Lexicographic order
  • $(a,i) > (b,j)$
    • if $a>b$ or $(a=b)\cap(i>j)$

class Bakery implements Lock{
    boolean[] flag;
    Label[] label;

    public Bakery(int n){
        flag = new boolean[n];
        label; = new Label[n];

        for (int i = 0; i<n; i++){
            flag[i] = false;
            label[i] = 0;
        }
    }

    public void lock(){
        flag[i] = true;
        label[i] = max(label[0],...,label[n-1])+1
        while (there exist another waiting thread and that thread's label is less than mine){/*wait*/}
    }

    public void unlock(){
        flag[i] = false;
    }
}

• This algorithm has no deadlock as there is always a thread with the earliest label

• First-Come-First-Served can be demonstrated by:

  • if $D_A \prec D_B$ then
    • $A$'s label is smaller
  • And
    • $write_A(label[A])\prec \\ read_B(label[A]) \prec \\ write_B(label[B]) \prec read_B(flag[A])$
  • So $B$ sees
    • smaller label for $A$
    • locked out while flag[A] is true.

• Mutual Exclusion can be shown by:

  • Suppose $A$ and $B$ are in the CS together
  • Suppose $A$ has the earlier label
  • When $B$ entered it must have seen:
    • flag[A] == false or label[A] > label[B]
    • But labels are strictly increasing so $B$ must have seen flag[A] == false
      • $Labeling_B \prec read_B(flag[A]) \prec write_A(flag[A]) \prec Labeling_A$
      • Which contradict the assumption that $A$ has the earlier label $\therefore$ impossible, $\therefore$ Bakery satisfies mutual exclusion.

Impracticality of the Bakery Algorithm

The Bakery Algorithm isn't widely used due to its impracticality stemming from its need for $N$ Distinct variables

Shared Memory

Shared read/write memory locations called Registers. Here we assume that all reads and writes are atomic

There are different types of registers:

• Multi-Reader-Single-Writer (MRSW)
• Multi-Reader-Multi-Writer (MRMW)
• There are also SRMW and SRSW but they are not pertinent

---

Theorem

At least $N$ MRSW registers are needed to solve $N$-thread deadlock-free mutual exclusion

---

Proof

Without $N$-MRSW registers, with N threads at least one thread won't be able to express intent to enter the CS, diagrammatically:

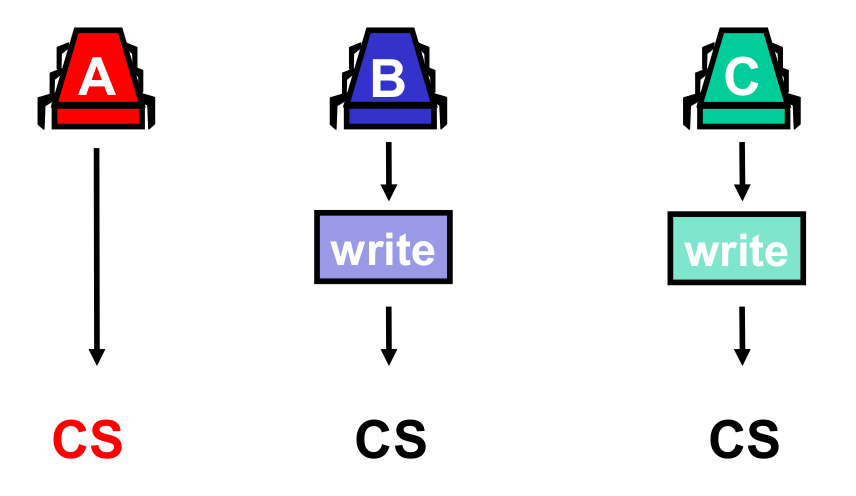
We cannot tell if $A$ is in the Critical Section

---

The bakery algorithm actually uses $2N$ MRSW registers

What if we use MRMW registers instead?

---

Bad News Theorem

At least $N$ MRMW registers are needed to solve deadlock-free mutual exclusion

---

i.e. it doesn't help us

---

Theorem, $N=2$

Deadlock-free mutual exclusion for $2$ threads requires at least $2$ MRMW registers

---

Proof

assume one register suffices & derive contradiction

---